数理音楽の風景（１）－不協和度曲線

2012年度卒業生から始めた当ゼミでの数理音楽なる分野，
その風景を数回シリーズでまとめてみよう．

準周期系の研究において連分数にまつわる力学系を扱うことが多かったことと，
はるか以前から音楽の仕組みに数理的仕組みが見え隠れしていると感じていたので，
ずっと取り扱いたいとは思っていたことだった．
そもそも音階の作り自体，繰り込み的な要素が多分にあるし，
その辺の感覚は連分数力学系そのものに由来する．
愛知教育大学学術情報リポジトリ

さて，その数理音楽のゼミでの取り扱い開始は2012年度7代目の卒業研究から．
ドレミファそーする？―音律の数理と音階の構成―
不協和度曲線から始まって，連分数展開による音階構成の仕組みまで触れた卒論．
とあるページでもこの卒論が紹介されているのをしばらく前に発見した．
sites.google.com
この卒論，元になった藤沢＋クックの論文*1
和音性の計算法と曲線の絵描き方 ―不協和度・緊張度・モダリティ―
の真似事から始まって，
不飽和度曲線で起こっている解析的な現象をちょっと数学的にきちんと書いてみた，
というものだった．
ただ，不協和度曲線の協和点でグラフが尖ってるといった特長があればいいものを，
そうもなっていなかったために，何らかの方法で協和点を解析的に特徴付けねば，
とでっち上げたのが第二種不協和度曲線だった．
tokidoki.hatenablog.jp

不協和度曲線の数理モデルのアイディアはこうだ．
まず，周波数の異なるsin波を同時に２つ鳴らし，
心理的な快不快の度合いを複数の被験者に採点してもらう．
その結果丁度半音階程度ずれたときが最も不快で，
そこを離れるに従い不快感は減っていったので，
この採点結果を適当な関数でモデル化する．それは例えば

であり，純音のドに対する別の純音の不協和度が以下．

しかし実際の楽器による楽音は複数の倍音が鳴っているため，
複合音の不協和度は純音の不協和度曲線をシフトして重ね合わせたものになるだろう，
つまり協和・不協和感覚に線形性が成り立っているだろう，という仮定を課すのである．

その結果，以下のような複合音に対する不協和度曲線が得られる．
例えば楽音のドに対する別の楽音の不協和度は↓

そして経験的に人々（正確には西洋音楽圏の人々*2）が協和すると感じる場所で
不協和度が下がっている，という尤もらしい説明ができる，というわけだ．
なお当たり前のことなのだが，この協和点の集合はFarey列にlog₂したものに他ならない．

特に完全五度である3/2倍音は常にオクターブに次いで最も協和度が高い．
そのことによってピタゴラスは現在ピタゴラス音律と呼ばれる，
音階づくりのルールを定めたのだった．
そしてそこから連分数力学系が絡む素敵な世界が広がるのだが，その話は次回以降へ．

音律と音階の科学―ドレミ…はどのようにして生まれたか (ブルーバックス)

*1:更にその大元にはPlomp と Leveltによる音楽心理実験があるのだ． R. Plomp and J. M. Levelt "Tonal Consonance and Critical Bandwidth" Journal of the Acoustical Society of America, 1965.

*2:実際，ハーモニーという概念を持たない民族圏の人々は例えば半音差で二音鳴らした場合と完全五度で鳴らした場合とで快不快感に特段の違いは起こらなかった，という実験結果がある．単旋律文化圏であった他ならぬ明治以前の日本人もそうだったのではなかろうか．

４独のCayley graphを描いてみた by Scratch

数独をテーマにしているゼミ生がいる．
当初は数独の難易度を測定する尺度を作れないか，
などといったことを夢見ていたが，
当人がそもそも数独を趣味にしていないようなので
そういった食指は動かなかったようだ．

じゃぁ何する，ってことになって，
そもそも数独は何通りあるのかをテーマにしようとなった．
もちろん参考書は↓

「数独」を数学する -世界中を魅了するパズルの奥深い世界-

けれど，数の並べ替えだけで9!＝362880あり，
更に盤の９色色分けの方法を考えると...と，ちょっと想像しただけでも手作業は無理．
しかし当人にプログラミング力があるわけでもなく，
そうすると人力でできるよう問題を簡単にするわけで，
数独likeなものとして４×４盤の４独を考えよう，となった．
実は４独盤は288通りだということが分かっていて，
４独盤集合を不変にする変換群（４独群と呼ぶことにしようか）
の位数も128と知られている．
（実際下に載せるBASICでしらみつぶしに調べたら128個だったし．）

これなら何とか形になるかも，と変換群の生成元をまずは固定して，
４独盤集合内の４独群の軌道を調べる，といったことを始めた．
で当人，手作業で盤を書いては試し書いては試しを繰り返していて，
何だかとても知的作業のように思えない．
いや，こうして泥臭い経験をする中から見えてくるものがあるわけだけど，
そして実際当人にも何か感覚的に見えてくるものがあったとのことだけど，
それにしても卒論提出間近にやる作業には思えない．

で，学生の卒論に託けて，４独群のシミュレーターをScratchで作ってみた．
４独変換群は３つの生成元で生成されることまでは卒論で示してあるので，
その３つの作用が動的に見えるようにしたものだ．

[4DOKU Group Simulator]
↓大変重いので，Turbo mode（Shiftキー押しながら緑の旗をクリック）で実行を．

そして，当然のことながら4DOKU Groupの「形」を見たいと思い，
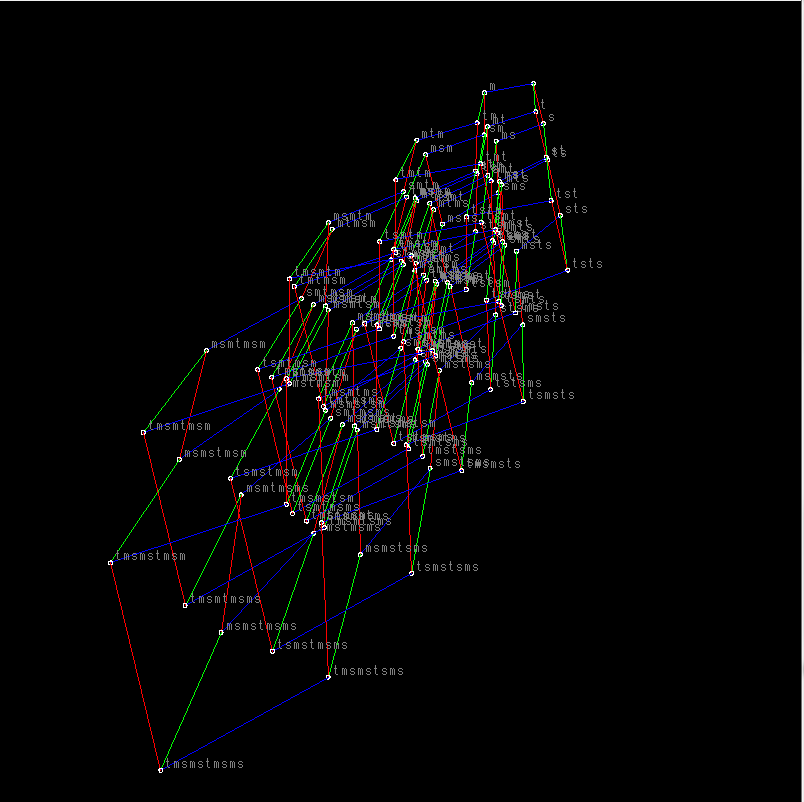
幸い３つの元で生成されているからそのCayley Graphを3Dで表示してみた．
[Cayley Graph of 4DOKU Group]
↓大変重いので，Turbo mode（Shiftキー押しながら緑の旗をクリック）で実行を．

しかし，下地となるCayley graphの接続状況などすべてScratchで行うのはちょいと厳しい．
ってことで，10進BASICでそのあたりはゴニョゴニョっと．

REM
REM [4doku group calculator]
REM ver. 2016/12/23
REM

DIM bd$(1 TO 4,1 TO 128),pm$(1 TO 23),typ$(1 TO 12),cg(1 TO 3,1 TO 128)
DATA "1243","1324","1342","1423","1432","2134","2143","2314","2341","2413","2431"
DATA "3124","3142","3214","3241","3412","3421","4123","4132","4213","4231","4312","4321"
FOR k=1 TO 23
   READ pm$(k)
NEXT k
DATA "1234341221434321","1234342121434312","1234342143122143","1243341221344321"
DATA "1243342123144132","1243341243212134","1234341223414123","1234341241232341"
DATA "1234341243212143","1243342121344312","1243342141322314","1243342143122134"
FOR k=1 TO 12
   READ typ$(k)
NEXT k

!LET bd$(1,1)="1234341221434321" !初期盤
LET bd$(1,1)="123456789abcdefg" !初期盤
LET bd$(2,1)="" !単位元

LET top=1
LET btm=1
LET idx=btm
PRINT USING "### [################] <#####################":idx,bd$(1,1),bd$(2,1)
DO
   PRINT "----";top;" to ";btm;"----"
   FOR k=top TO btm
      LET a0$=bd$(1,k)
      LET g$=bd$(2,k)
      !σ
      IF g$(1:1)<>"s" THEN
         LET a$=sigma$(a0$)
         LET ss=search(a$,idx)
         IF ss=0 THEN
            LET idx=idx+1
            LET bd$(1,idx)=a$
            LET bd$(2,idx)="s"&g$
            PRINT USING "### [################] <#####################":idx,a$,bd$(2,idx)
            LET bd$(3,k)=bd$(3,k)&"s"&STR$(idx)&","
         ELSE
            LET bd$(3,k)=bd$(3,k)&"s"&STR$(SS)&","
         END IF
      END IF
      !μ
      IF g$(1:1)<>"m" THEN
         LET a$=mu$(a0$) 
         LET ss=search(a$,idx)
         IF ss=0 THEN
            LET idx=idx+1
            LET bd$(1,idx)=a$
            LET bd$(2,idx)="m"&g$
            PRINT USING "### [################] <#####################":idx,a$,bd$(2,idx)
            LET bd$(3,k)=bd$(3,k)&"m"&STR$(idx)&","
         ELSE
            LET bd$(3,k)=bd$(3,k)&"m"&STR$(SS)&","
         END IF
      END IF
      !τ
      IF g$(1:1)<>"t" THEN
         LET a$=tau$(a0$)
         LET ss=search(a$,idx)
         IF ss=0 THEN
            LET idx=idx+1
            LET bd$(1,idx)=a$
            LET bd$(2,idx)="t"&g$
            PRINT USING "### [################] <#####################":idx,a$,bd$(2,idx)
            LET bd$(3,k)=bd$(3,k)&"t"&STR$(idx)&","
         ELSE
            LET bd$(3,k)=bd$(3,k)&"t"&STR$(SS)&","
         END IF
      END IF
       
   NEXT k
   LET top=btm+1
   LET btm=idx
LOOP UNTIL top>btm

PRINT
PRINT

! Cayleyグラフの為の接続状況一覧-----------------
FOR k=1 TO btm
   PRINT USING "### [################] <########## <"&REPEAT$("#",40):k,bd$(1,k),bd$(2,k),bd$(3,k)
   LET g$=bd$(2,k)
   LET ln=1
   DO
      SELECT CASE g$(1:1)
      CASE "s"
         LET cg(1,k)=cg(1,k)+ln
      CASE "m"
         LET cg(2,k)=cg(2,k)+ln
      CASE "t"
         LET cg(3,k)=cg(3,k)+ln
      CASE ELSE
      END SELECT
      LET g$(1:1)=""
      LET ln=ln*1.2
   LOOP UNTIL g$=""
NEXT k

PRINT
PRINT

! 各gの12typeへの作用の様子----------------------
FOR k=1 TO btm
   LET g$=bd$(2,k)
   PRINT USING "[### <"&REPEAT$("#",10)&"] ":k,g$;
   LET cr$=""
   LET ct=0
   FOR t=1 TO 12
      LET res$=typ$(t)
      FOR l=1 TO LEN(g$)
         SELECT CASE g$(l:l)
         CASE "s"
            LET res$=sigma$(res$)
         CASE "m"
            LET res$=mu$(res$)
         CASE "t"
            LET res$=tau$(res$)
         CASE else
         END SELECT
      NEXT l
      LET res$=std$(res$)
      LET cr$=cr$&USING$("##",t)
      IF res$=typ$(t) THEN
         LET cr$=cr$&"=O,"
         LET ct=ct+1
      ELSE
         LET cr$=cr$&"=X,"
      END IF
   NEXT t
   LET bd$(4,k)=STR$(ct)
   PRINT USING ">## ":bd$(4,k);
   PRINT "(";cr$;")"
NEXT k

PRINT

! |X^g|=k となる g の表示--------------------------
FOR t=1 TO 12
   LET cr$=""
   LET ct=0
   FOR k=1 TO btm
      IF bd$(4,k)=STR$(t) THEN
         LET ct=ct+1
         LET cr$=cr$&bd$(2,k)&","
      END IF
   NEXT k
   IF ct>0 THEN
      PRINT "{g|X^g|=";t;"}=";ct;"{";cr$;"}"
   END IF
NEXT t

!FOR k=1 TO btm
!   PRINT bd$(2,k)
!NEXT k
!FOR k=1 TO btm
!   PRINT bd$(3,k)
!NEXT k

! Cayleyグラフ描画---------------------------------
! [4]←→[6] [8]↑[5]↓ [a][z]ｚ方向
! [s] zoom in [x] zoom out
LET wmax=8
SET COLOR MIX(0) 0,0,0
SET COLOR MIX(1) 1,1,1
SET TEXT COLOR 8
SET WINDOW -wmax,wmax,-wmax,wmax
LET dt=0.01
LET QX=-0.6
LET QY=-3
LET QZ=1.8
LET OX=3.5
LET OY=7
LET sw=1
DO
   mouse poll mx,my,left,right
   LET ky$=""
   CHARACTER INPUT nowait:ky$
   SELECT CASE ky$
   CASE "8"
      LET dx=MIN(0.1,dx+dt)
   CASE "5"
      LET dx=MAX(-0.1,dx-dt)
   CASE "4"
      LET dy=MAX(-0.1,dy-dt)
   CASE "6"
      LET dy=MIN(0.1,dy+dt)
   CASE "a"
      LET dz=MIN(0.1,dz+dt)
   CASE "z"
      LET dz=MAX(-0.1,dz-dt)
   CASE "s"
      LET wmax=wmax/1.01
   CASE "x"
      LET wmax=wmax*1.01
   CASE " "
      LET sw=1-sw
   CASE ELSE
   END SELECT
   SET WINDOW -wmax,wmax,-wmax,wmax
   LET QX=QX+dx
   LET QY=QY+dy
   LET QZ=QZ+dz
   LET dx=dx*0.95
   LET dy=dy*0.95
   LET dz=dz*0.95
   IF left=1 THEN
      LET OX=mx
      LET OY=my
   END IF
   SET DRAW mode hidden
   CLEAR
   FOR k=1 TO 128
      LET ed$=bd$(3,k)
      LET X0=rotX(cg(1,k),cg(2,k),cg(3,k))
      LET Y0=rotY(cg(1,k),cg(2,k),cg(3,k))
      SET LINE COLOR 1
      DRAW circle WITH SCALE(wmax/200)*SHIFT(X0,Y0)
      IF sw=1 THEN
         PLOT TEXT ,AT X0+wmax/100,Y0 ,USING"<##########":bd$(2,k)
      END if
      DO UNTIL ed$=""
         LET l=POS(ed$,",")
         LET idx=VAL(ed$(2:l-1))
         IF idx>k THEN
            SELECT CASE ed$(1:1)
            CASE "s"
               LET cl=4
            CASE "m"
               LET cl=2
            CASE "t"
               LET cl=3
            END SELECT
            SET LINE COLOR cl
            LET X1=rotX(cg(1,idx),cg(2,idx),cg(3,idx))
            LET Y1=rotY(cg(1,idx),cg(2,idx),cg(3,idx))
            PLOT LINES: X0,Y0;X1,Y1
         END IF
         LET ed$(1:l)=""
      LOOP
   NEXT k
   SET DRAW mode explicit
LOOP UNTIL left*right=1

REM -----------------------------------------------
REM 呼び出し関数
REM -----------------------------------------------

! 一致する盤を探す
FUNCTION search(S$,midx)
   LET kk=1
   LET search=0
   DO
      IF bd$(1,kk)=S$ THEN
         LET search=kk
         LET kk=midx
      END IF
      LET kk=kk+1
   LOOP UNTIL kk>midx   
END FUNCTION

! 作用σ
FUNCTION sigma$(i$)
   LET a$=i$         
   LET b$=a$(5:8)
   LET a$(5:8)=""
   LET sigma$=b$&a$
END FUNCTION

! 作用μ
FUNCTION mu$(i$)
   LET a$=i$         
   LET b$=a$(9:16)
   LET a$(9:16)=""
   LET mu$=b$&a$
END FUNCTION

! 作用τ
FUNCTION tau$(i$)
   LET a$=i$(1:1)&i$(5:5)&i$(9:9)&i$(13:13)
   LET a$=a$&i$(2:2)&i$(6:6)&i$(10:10)&i$(14:14)
   LET a$=a$&i$(3:3)&i$(7:7)&i$(11:11)&i$(15:15)
   LET tau$=a$&i$(4:4)&i$(8:8)&i$(12:12)&i$(16:16)
END FUNCTION

! 盤の標準化
FUNCTION std$(i$)
   LET s$="1234"
   LET v=VAL(i$(1:1))
   LET s$(v:v)=STR$(1)
   LET v=VAL(i$(2:2))
   LET s$(v:v)=STR$(2)
   LET v=VAL(i$(5:5))
   LET s$(v:v)=STR$(3)
   LET v=VAL(i$(6:6))
   LET s$(v:v)=STR$(4)
   LET st$=""
   FOR kk=1 TO 16
      LET v=VAL(i$(kk:kk))
      LET st$=st$&s$(v:v)
   NEXT kk
   LET std$=st$
END FUNCTION

FUNCTION rotX(X,Y,Z)
   LET rotX=(X*COS(QZ)+Y*SIN(QZ))*COS(QY)+((X*SIN(QZ)-Y*COS(QZ))*SIN(QX)+Z*COS(QX))*SIN(QY)+OX
END FUNCTION

FUNCTION rotY(X,Y,Z)
   LET rotY=(-X*SIN(QZ)+Y*COS(QZ))*COS(QX)+Z*SIN(QX)+OY
END FUNCTION

END

Scratch で置換計算機

じゃ～ん．

やっぱり今年もこういう季節だね．
とはいえ，今年，そして来年度は会議やら会議やら，それから会議やらで
卒論にあまりかまってられない事態ではあるが．
おかげで，今年は赤を入れるタイミングが大幅に遅れている．
それでもそろそろ形になってくれないかなぁ～．

ってことで，困ったときのプログラミングでお茶を濁す作戦．
今年も幾つか卒論用に作ってきたところだ．
その一つ，置換計算機を紹介しよう．

[使い方]
左にならぶ紫玉クリックで巡回置換表現での置換をセット．
例えば 123,45,67 と入力すれば置換 (1 2 3)(4 5)(6 7) をセットしたことになる．
置換表示に使える文字は123456789abc...xyzの35文字だ．
それぞれの紫玉には上から順にA,B,C,...と置換に名前がついており，
15個の置換まで登録できる．

CALCボタンを押すと計算して欲しい置換の積が，ABCBBAといった具合に入力できる．
ただし，積の解釈は右から左．A=(1 2 3),B=(2 3 4)ならAB=(1 2)(3 4)だ．
計算の結果は ,1,23,465, などと出るが，その意味は(2 3)(4 6 5)だ．

なお，max スライドバーは置換に現れる文字種の最大数を指定している
（計算を速めるため）．したがってスライドバーの最大は35だ．

「蜘蛛の糸」展＠豊田市美術館

行ってきました，今年のトリエンナーレ関連最後のシリーズ．
「蜘蛛の糸」展＠豊田市美術館．

塩田千春氏の作品．
今回の展覧会のメインの作品だろう．これは撮影ＯＫだった．

そして氏の作品，実は以前「てくてく現代美術世界一周」でお会いしている．
tokidoki.hatenablog.jp

↓木漏れ日ならぬ「クモれ日」．

そしてどこもかしこも黒い糸で覆われていた．

戸谷成雄「雷神」

で，せっかくの現代アート展でもあるのだけど，今回は殆ど撮影不可だった．
芥川の「蜘蛛の糸」をからくり時計で見せるグロテスクな作品とか，
蜘蛛の糸から連想される奇妙な世界やら，色々と面白いものがあったのだけどね．

仕方ないので，豊田市美術館の風景を．





ここまでILCE-6000+SEL1670ZF4.0にて．

で，雰囲気の良い木漏れ日があったのでレンズをSEL35F1.8OSSに変えて．

そうそう，１枚ぐらいリアルな蜘蛛を．これ胴体だけで5cm近くあったよ．

あいちトリエンナーレ2016―栄最終調査１ カンパニー・ディディエ・テロン

あいちトリエンナーレも明日で終了．
本日は夜に小杉武久「MUSIC EXPANDED#1」があるのと，
名古屋市美術館でカンパニー・ディディエ・テロンによる屋外パフォーマンスがある．
色々と考えさせられることとなった小杉氏のパフォーマンスは別枠で語るとして，
まずはこのケッタイな屋外パフォーマンスを紹介．

10:30，なかなか撮影にはいい場所を確保した．
11:00，いよいよご登場．演目は「膨らんだ冒険」から「Air」．

で，階段を降りて行って，






なにやらひそひそ話？

でーん．なんじゃ，このケッタイな埴輪．





で，ダンスが始まる．あ，無音だけど．


サービス，サービスぅ（葛城ミサト風に）

あれ，疲れた？

しゃがむとまた面白いフォルムになる．

しかし暑そう．

そしてシュールな時間は終焉を迎える，

巨大なおしりと共に．


およそ30分のパフォーマンス，あるいはバカバカしく見えるかもしれなくても，
突き抜ければアートになる．もちろん会場の誰もバカバカしいなんて思っていない．
大いなる喝采に包まれた．

なお，14:30から今度は長者町界隈でパフォーマンスするそうなので，
長者町会場をフラフラ．その日は長者町繊維街の祭りだった．

何か色んなものが歩いていた．




そして14:30をやや過ぎたころ，彼らが再び現れる．大勢に囲まれて．






しかしもう，人だかりで全く見えないので，諦めて県美へ．
おっとその前に長者町会場で再度撮影したものを．
既に，過去記事で二回にわたり紹介してはあるけど，
改めて見るとまだまだ色んなものが見えてくる．
tokidoki.hatenablog.jp
tokidoki.hatenablog.jp

（栄N-52）寺田就子
「静かで大好きな小空間」を形にした感じで，三度訪れたお気に入り．
同様な理由で今村文さんの静謐な時間を感じる作品も好きだった．

（栄N-49）端聡
水の循環を表現した作品だけど，よく見ると蒸発した気体は水には戻っていなかったね．


県美の入り口には名古屋・岡崎・豊橋３会場で企画されていたJoao Modeの作品が結集．
あれ，でも塊は二つだね．

お目当ての「MUSIC EXPANDED#1」まで三時間ほどある．
まぁ，最後にもう一度県美の作品をじっくり見よう．

（県美N-13）大巻伸嗣
10日ほど前からこの作品に足を踏み入れて良いようになった．
だからすっかり色が消えていた．あ，でもあの真っ白の柱の裏には作品があったんだね．
今回もう一度来てやっと見つけられたよ．

（県美N-17）田島秀彦
岡崎会場では石原邸の庭を借景とした作品があったのだが，
tokidoki.hatenablog.jp
そして夏に来た時には１２階の回廊は暑くてまともに見てられなかったのだが，
今回ようやくタイルをきちんと撮影できた．

さてさて，これで今回のトリエンナーレは見納め．
最後に小杉武久「MUSIC EXPANDED#1」を体験するわけだが，
もうパフォーマンス中，そしてその後，色々思ったりしたわけだ．
その一端を言葉にするなら，
「分かってるつもりになるということは，どれほど世界を知らずに過ごすことになるのか」
ということだ．
この話は別の機会にまとめよう．

あいちトリエンナーレ2016 虹のキャラヴァンサライ 創造する人間の旅

あいちトリエンナーレ2016オフィシャルガイドブック (ぴあMOOK)