まず初めに,講義「統計とコンピュータ」で本年度の3年生102人から得たあるデータを紹介しよう.
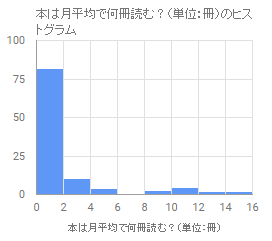
これはひと月平均本を何冊読むか?に対する結果だ.
(Google formによる調査はこんなふうにその場でグラフにまでしてくれて便利だ.)
因みに中央値は0.1冊とも教えてくれた.つまり,ほとんどが「全く読まない」ということだ.
自分が属しているのは数学教育の講座で,だから自称「理系」の学生らが集まる学科である.
赴任した頃の十数年前でも,教育学部であるにもかかわらず「本を読まない」,
正確には「本が読めない」学生が少なからずいたことは知っていた.
そんな彼らが一体どんな顔をして子どもたちに読書を勧め,習慣化させるのか
当時から不思議でならなかったことを思い出した.
(そういえばその当時,「国語のできない文系」などといって学生を揶揄していたものだ.)
そして現在,改めて調査をしてみると予想はしていたものの,愕然とする結果となった.
今日は講座で行っている教員採用試験の為の面接練習会に面接官役として出たわけだが,
どうやら戦後の昭和の言葉すら通じなくなってきている事態にあることに改めて直面した次第.
本日通じなかったのは「困ったときはお互い様」そして「卆なく答える」.
いずれも良い意味なのか悪い意味なのか,といったニュアンスそのものが分からなかったらしい.
(そして実は前者の言い回しは最近30代の同僚にも使ったことを思い出し,
ひょっとするとニュアンスを間違って取られているかもしれない,
などと面接練習中に密かにゾッとしていた.いや,杞憂に過ぎないだろうが.)
もちろん,言葉は生き物であるし,時代と共に変わってしまう宿命にあることは承知しているつもりだ.
自分だって自分よりずっと上の年代からすればヘンテコな日本語を使っているのだろう.
例えば「全然」という副詞.
「全然大丈夫」なる表現は二度折れ曲がって間違いでもないともいえる.
かつてこの熟語が中国から輸入されたとき,それは「全く」の意味だったそうだ.確かに字義通り.
漱石の時代でも「君の意見に全然同意するよ」などと言っていた.
それが戦後教育の中で「全然」は否定語の前につけるが正しい,としてきたのだそうだ.
そしていつの時代も古いモノを壊して遊ぶのが若い世代の特性であって,
言葉もわざと前時代では間違ったとされる使い方を敢えてする.
「全然だめだ」という言い方に慣れた人々の中,
「全然いける」などと言ってその若干の違和感を楽しむ.
そうやって遊んでいるうちに「全然」が「とても」の意味に解釈され始め,
「全然楽しい」などと使うようになる.
こういった変遷は言葉遊びから来るもので,ライブ感があって楽しい.
しかし一方で,「~することができる」の多用には,
現代日本の歪み,あるいは病いが垣間見える,というのが持論だ.
tokidoki.hatenablog.jp
(その他気になっている言葉は多数ある.
政治家が使う「粛々と」「説明する」「しっかりと」,
また一般人がしきりにつかう「させていただく」,「意識高い系」の自虐的使用,
そしてすっかり浸透した「癒し」や「感動した」の安易な使用.
いつかこの辺りのことも書きたいけれど,まだ醸造中だ.)
話が逸れた.「本が読めない」教育学部の学生のことだった.
この事態は世間が言う「若者が本を読まない」を問題と捉えることとは
少々質的に違うように感じる.というのもそこに「教育学部の」がつくからだ.
教育現場はやはり"生き物"であるし,
目まぐるしく変わる事態への俊敏な対応が常に迫られる.
けれど一方では,人類が(とまでは行かずとも先人が)歩いてきた道を
生き生きと伝える場でなくてはなるまい.
つまり教育現場は子どもの目を過去と未来,両方に拓かせるはずの場所だ.
教育現場における不易流行,あるいはもっとシンプルに温故知新だ.
(もちろん教育現場だけがその責務を負う,という訳ではないものの,
地域共同体がすっかり壊れてしまった現代―だから「お互い様」が分からなかったのか―
やはり最後の砦としての役割は大きい.)
その一方の扉であるはずの書物をやがて現場教員となる学生が「読めない」となると,
教員自身,先人の叡智を持たぬまま,まる裸で現代と闘うに等しく,
同時に眼前の子どもたちにも根っこの無い知識を切り売りして過ごすことになる.
こうして歴史を持たない子どもたちが拡大再生産されていくわけだ.
そしてこの事実は日本国民の,
真の意味での個人の確立と市民への成長を大いに妨げてきたのだと思う.
(この点については,「個人」の概念そのものを条文から消し去ろうとしている,
"腹立たしい"自民党憲法草案へ話はつながるのだけど,これもまたいずれ.)
さて.ひたすら場の空気だけを読んでそれこそ「卆なく」その日暮らしをする世代.
昭和言葉(もう大和言葉まで遡ることもできない)ですら通じにくくなっているのは,
地域共同体が壊れたことと同時に,やはり少し前の本を読まないからだと単純に思う.
例えばではあるが,2chをはじめとするネットスラングの世界は,
始めた側にとってはフィネガンズ・ウェイクばりの言葉遊びだったのだろうけど,
多感な時期にずっとそういった「崩した/壊した」言葉に囲まれて育った世代が増えるとき,
しかもその文化の変遷は数年単位で起こる故,
彼らの智慧の基盤はとても脆弱なものとならざるを得ない.
時代とはいえ,それにしてもね.
「最終的に立ち戻る場所がYahoo!の知恵袋のみ」という教員には
やっぱり教わりたくないなぁ...
因みに↑の著者は数学者.
藤原先生のデビュー作「若き数学者のアメリカ」を読んだ,ネット社会未明の時代が懐かしい.















