ミイラ取りがすっかりミイラになった感のある前回のエントリー.
tokidoki.hatenablog.jp
前回の結果はまとめると
\begin{equation}
2\sum_{k=a}^x k=\sum_{k=a}^b k
\end{equation}
を満たす組は互いに素な
によって,
何れかが偶数なら
\begin{equation}
(a,b,x)=\left((p+q)^2-2q^2,(p+q)^2-2p^2,p^2+q^2\right),
\end{equation}
何れも奇数なら
\begin{equation}
(a,b,x)=\left(\frac{(p+q)^2-2q^2}{2},\frac{(p+q)^2-2p^2}{2},\frac{p^2+q^2}{2}\right)
\end{equation}
と表されるということだった.こうしてあらゆる解がパラメータで表現できると分かったものの,特定の解だけ抜き出そうとするとそれはそれでまた話が膨らむようなのだ.例えば
と固定した場合,どのような
ならば
\begin{equation}
(p+q)^2-2q^2=1
\end{equation}
を満たすだろうか?といった問題に変わる.
実はこの話,ラマヌジャンが直感的に解いたという逸話があるそうで,それは
\begin{equation}
2\sum_{k=1}^x k=\sum_{k=1}^b k
\end{equation}
の解を
の連分数展開を使って求める話だなのだが,先に進む前に今回は連分数展開の力学系としての私なりの解釈を書き留めておこうと思った.というのも連分数が出てくる度,その見方を思い出すのに時間がかかってきたからだ.
無理数
\begin{equation}
\alpha=[a_0;a_1,a_2,\dots]=a_0+\frac{1}{a_1+\displaystyle\frac{1}{a_2+\cdots}}
\end{equation}
となっているとする.これは帰納的に
\begin{equation}
\alpha_{n}=a_n+\frac{1}{\alpha_{n+1}},\ a_n=\lfloor\alpha_n\rfloor
\end{equation}
つまり
\begin{equation}
\alpha_{n+1}=\frac{1}{\alpha_n-a_n},\ \alpha_0=\alpha
\end{equation}
とも表せる.要するに
\begin{equation}
T(x)=\frac{1}{x-\lfloor x\rfloor}
\end{equation}
なる力学系を考えているに他ならない.が,近似分数を思うならば,これを分母分子を意識した形で書き直したい.傾き
\begin{equation}
e_1+xe_2=(e_1+ae_2)+(x-a)e_2=e'_2+(x-a)e'_1
\end{equation}
なる変換,つまり
\begin{equation}
(e_1\ e_2)\mapsto (e'_1\ e'_2)=(e_1\ e_2)\begin{pmatrix} 0 & 1\\ 1 & a \end{pmatrix}
\end{equation}
ならば図形的にもやっていることが分かりやすい.
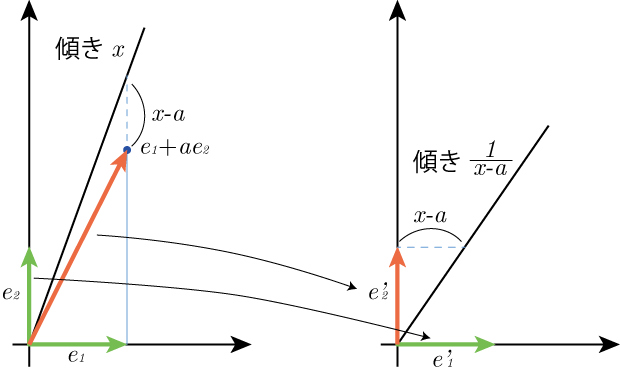
したがっての連分数展開
] は基底変換
\begin{equation}
(e_1\ e_2)\mapsto(e'_1\ e'_2)=(e_1\ e_2)\begin{pmatrix} 0 & 1\\ 1 & a_0 \end{pmatrix}\\
(e'_1\ e'_2)\mapsto(e''_1\ e''_2)=(e'_1\ e'_2)\begin{pmatrix} 0 & 1\\ 1 & a_1 \end{pmatrix}
=(e_1\ e_2)\begin{pmatrix} 0 & 1\\ 1 & a_0 \end{pmatrix}\begin{pmatrix} 0 & 1\\ 1 & a_1 \end{pmatrix}
\end{equation}
を繰り返していく操作と読み替えられる.さらに回目の基底変換では
\begin{equation}
(e^{(n)}_1\ e^{(n)}_2)=(e^{(n-1)}_1\ e^{(n-1)}_2)\begin{pmatrix} 0 & 1\\ 1 & a_{n-1} \end{pmatrix}
=(e_1\ e_2)\begin{pmatrix} 0 & 1\\ 1 & a_0 \end{pmatrix}
\begin{pmatrix} 0 & 1\\ 1 & a_1 \end{pmatrix}\cdots
\begin{pmatrix} 0 & 1\\ 1 & a_{n-1} \end{pmatrix}
\end{equation}
と書けるのでが分かる.さらに
\begin{equation}
e^{(n+1)}_2=e^{(n)}_1+a_ne^{(n)}_2=a_ne^{(n)}_2+e^{(n-1)}_2,
\end{equation}
したがって
\begin{equation}
e^{(n+1)}_1=e^{(n)}_2=e^{(n-1)}_1+a_{n-1}e^{(n-1)}_2=a_{n-1}e^{(n)}_1+e^{(n-1)}_1
\end{equation}
と書けるのでと表せば,近似連分数に関する漸化式
\begin{equation}
q_{n+1}=a_nq_n+q_{n-1}
\end{equation}
および
\begin{equation}
p_{n+1}=a_{n-1}p_n+p_{n-1}
\end{equation}
が得られる.こうして近似分数
\begin{equation}
\frac{q_n}{p_n}=[a_0;a_1,a_2,\dots,a_{n-1}]
\end{equation}
にたどり着く.
ところで この行列表示
\begin{equation}
(e^{(n)}_1\ e^{(n)}_2)
=(e_1\ e_2)\begin{pmatrix} 0 & 1\\ 1 & a_0 \end{pmatrix}
\begin{pmatrix} 0 & 1\\ 1 & a_1 \end{pmatrix}\cdots
\begin{pmatrix} 0 & 1\\ 1 & a_{n-1} \end{pmatrix}
=(e_1\ e_2)\begin{pmatrix} p_{n-1} & p_n\\ q_{n-1} & q_n \end{pmatrix},
\end{equation}
連分数近似に関する諸性質が容易に得られるのが嬉しい.例えば行列式が
\begin{equation}
\begin{vmatrix} p_{n-1} & p_n\\ q_{n-1} & q_n \end{vmatrix}
=\begin{vmatrix} 0 & 1\\ 1 & a_0 \end{vmatrix}
\begin{vmatrix} 0 & 1\\ 1 & a_1 \end{vmatrix}\cdots
\begin{vmatrix} 0 & 1\\ 1 & a_{n-1} \end{vmatrix}
=(-1)^n
\end{equation}
となって,
\begin{equation}
p_{n-1}q_n-p_nq_{n-1}=(-1)^n
\end{equation}
が得られ,隣接近似分数の距離が
\begin{equation}
\left|\frac{q_n}{p_n}-\frac{q_{n-1}}{p_{n-1}}\right|=\left|\frac{p_{n-1}q_n-p_nq_{n-1}}{p_np_{n-1}}\right|=\frac{1}{p_np_{n-1}}
\end{equation}
と分かる.あるいはこの行列表示を転置すると
\begin{equation}
\begin{pmatrix} 0 & 1\\ 1 & a_{n-1} \end{pmatrix}
\begin{pmatrix} 0 & 1\\ 1 & a_{n-2} \end{pmatrix}\cdots
\begin{pmatrix} 0 & 1\\ 1 & a_0 \end{pmatrix}
=\begin{pmatrix} p_{n-1} & q_{n-1}\\ p_n & q_n \end{pmatrix},
\end{equation}
となるが,これは連分数
v[a_{n-1};a_{n-2},\dots,a_0=\frac{q_n}{q_{n-1}}
\end{equation}
が分かり,同時に行列表示の第一列の意味を考えれば
\begin{equation}
[a_{n-1};a_{n-2},\dots,a_1]=\frac{p_n}{p_{n-1}}
\end{equation}
も分かる.


















